ETH hedging in DeFi: new back-test results
Perma hedging with put options priced with a Black-Scholes engine.
Introduction
Last week we looked at creating a permanent hedge position on ETH using Hegic’s beta version, with a very basic pricing engine. We saw that with that engine, the systematic hedging system nearly always won.
This week, we look at a more sophisticated implementation of the hedging system, with a Black Scholes dynamic approach to pricing.
Neither Hegic nor Opyn can guarantee these specific prices, but the results here can serve as a good benchmark for what to expected. In this post we look at the results of this updated strategy model, and compare it against simply holding.
Pricing approach
The Black-Scholes price engine isn’t perfect, but many market participants use it to measure current market conditions.
Here’s the basic idea: you submit some parameters (Current Price, Strike Price, Volatility, and Time to Maturity), and the system works out a price.

It’s key to understand that options are traded in the market with open pricing. Participants exchange at freely agreed prices, without obeying any model.
For that reason, typically the model is used as follows:

People work out “implied volatility”, from option traded prices seen in the market place.
Volatility input to the model
DeFi Options on ETH only became available recently, so we don’t have historical implied volatility, nor historical put-contract pricing.
We will try to use the next best thing. We’ll experiment with two approaches:
Historical Volatility: We will feed into Black-Scholes historical vol for the last cycle, and work out a price from it. Then we’ll add a 20% bias on top. This approach looks BACK to get to volatility.
Realized volatility: We will feed the actual realized volatility for the coming cycle (since we can magically see the future during the back test). Then we’ll add a 20% bias on top. This approach looks FORWARD to get to volatility.
Side Note: The first approach would be directly implementable in DeFi: An AMM (automatic market maker) could be created, that used the last periods’ volatility to “make” a price. It should be studied, what the LP’s P&L look like, when supplying liquidity a Black-Scholes “uniswap”.
The second approach, gives us a perhaps a more reliable representation of how the strategy would have worked in real life pricing. Implied vol and realized vol have shown to have a reasonably consistent bias in S&P VIX for example.

Implied Volatility = Realized Volatility + “the Delta” in the graph
This shows that implied vol on average behaves like realized vol + a certain bias. We can replicate that, by looking at the actual realized vol, and then adding an additional bias on top, to create conservatively “expensive” option, to test the strategy with. The higher the volatility, the higher option prices.
In the interest of length, in this post we’ll be looking at the results from the second approach only. In our testing both models behaved reasonably similarly. More info available in A/B testing both volatility models.
In summary: the results below use option pricing based on realized volatility.
Gas costs
Based on feedback on the previous back-test, we now account for Gas costs associated with the deployment of the strategy. Here’s the basic approach:
We take a number of transactions per cycle as a parameter (2tx for example = 1 tx to buy put, 1tx to exercise option, for example)
We look at actual ETH fees per tx paid historically at each expiration/refresh time.
We multiply both by the ETH historical price at expiration/refresh time.
This feels very realistic. In our mind, this transaction probably could be optimized to 1 or 2 tx per cycle, no more.
Results
The system behaves as expected. It outperforms during down-turns, it under-performs in market rallies.
Let’s look at one particular example, taking the period from Jan 2017 to Jan 2020:

This is a particular trading path starting on one particular date, and finishing on a particular date too.
Now let’s look at 200 different entry exit paths within this same total period, to see whether timing in and out mattered:
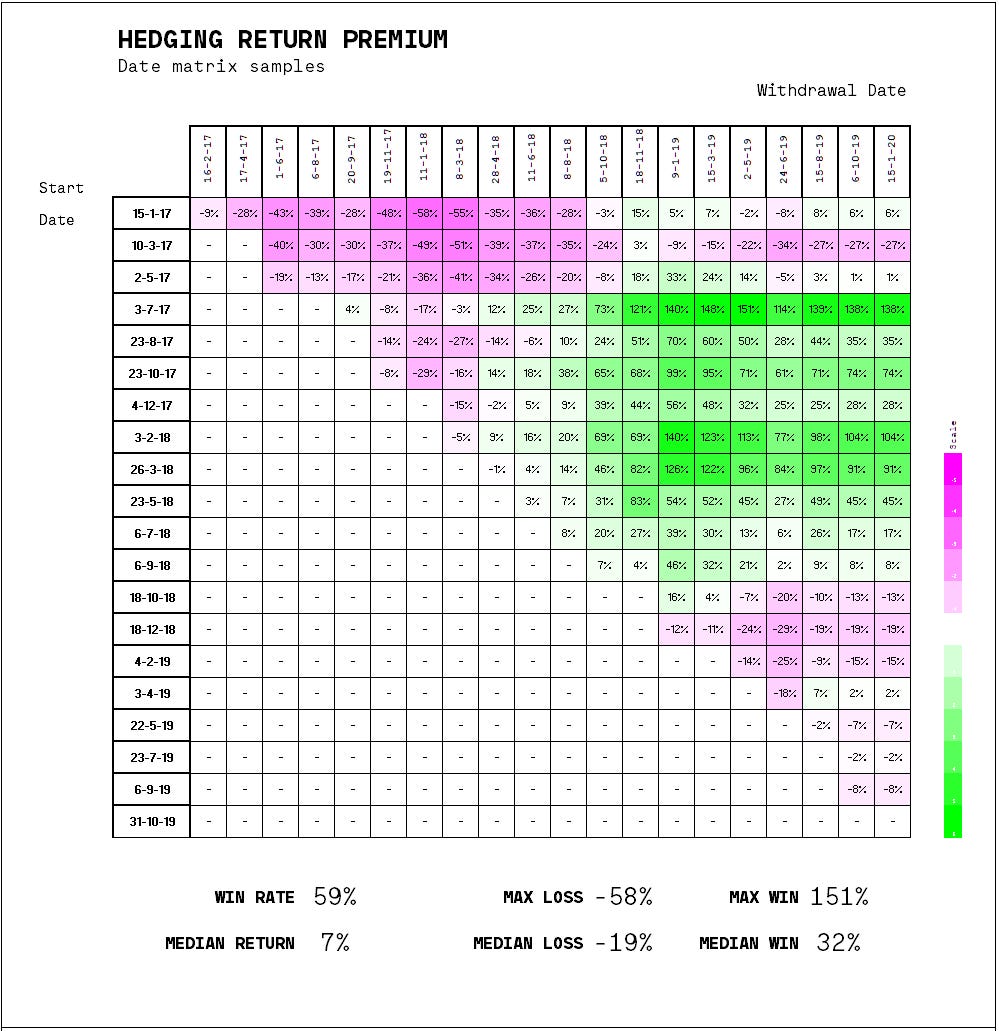
As you can see, the strategy is clearly time sensitive. Let’s look at four different time periods and see the general results.
General patterns
Here’s a high level summary of how the strategy behaved from 2017 to 2020.

Here’s a numerical summary of that same data:

This is obviously only one slice of the possible results, with a very specific system parametrization (eg. 0,5 contracts per ETH hedged, 30 day refresh cycle).
Summary: Generally speaking, we see this could be an interesting instrument for people looking to have their savings insured, if they strongly believe a down-turn is coming. More research needed with the strategy parametrization.
Observations on parameters
Here’s what we’ve seen playing with inputs.
Timing: The start of the period is plays a big role. Starting with a highly volatile parabolic advance, makes the system underperform.
Hedging lever: With higher contracts per ETH (1+), the system can have fatal total wipe-out losses, in extended periods of price increases.
Cycle length: Having trialed from 7 to 90 days periods, over sufficiently long periods of time, the sampling doesn’t seem to affect results (very different from last time!!!).
Tx costs: We played from 0 to 50 Tx per cycle, and our conclusion was that from 1Tx to 5Tx per cycle, normally price and vol are still a way more dominant factor.
General take-aways
Hedging is great if you catch a downfall, or a black-swan. Very high gains of over 100% observed in those periods, even at cautious parameters. 300%+ returns possible.
Hedging can be risky as a permanent strategy. Even at cautious settings, losses of 65% observed in periods of price growth. It’s unclear whether a hedging makes sense as a perma-strategy. At some more aggressive hedging settings, strategy can wipe out-player.
More research needed on the strategy itself. Optimization opportunities, for example in using Kelly Criterion, and buying OTM puts instead of ATM, to improve performance.
Regardless of the ultimate strategy, we think these instruments will eventually be available.
We’re very excited about the idea of being able to send ETH to a contract, and have trustless certainty that a risk management strategy will be applied to it unstoppably, permissionlessly. All of it built on top of other reliable DeFi tech. Very interested in people’s ideas around this topic, and DMs open.
How would one go about building a project like this in the age of DeFi? How would you finance it, govern it, risk/reward from it? That’s what we plan on exploring in the coming posts. Subscribe to get notifications!
Would love to hear people’s thoughts.
Thank you to the Opyn and Hegic teams for their time reviewing early drafts of this article, and particularly to Opyn for their extensive comments on approaches to volatility pricing.
Share and help content spread!



